信道合并

将$N$个独立信道$W$通过变换使之变为一个具有“集体意义”的信道$W_N$，这里“集体意义”的产生来源于变换，而变换遵循固定的规则。
首先，变换是一个递归过程。对于$N(N=2n)$个独立信道$W$，想要将其变为一个具有“集体意义”的信道$W_N$需要进行$n$次信道操作，每次信道操作都将$N$个信道变为$N/2$个小型的信道集合体，这样通过递归$N$—>$N/2$—>……—>$2$—>$1$就可以实现$N$个信道的合并。每次信道操作又分为两个部分：

对信道输入向量的运算
譬如在B-DMC信道中，输入向量服从等概率分布，我们假设输入向量为$u_1^N$。对它进行的操作为$s_{2i-1}=u_{2i-1} \oplus u_{2i}$, $s_{2i}=u_{2i}$。
置换操作
对于上一步得到的向量$s_1^N=(s_1,s_2,\cdots,s_N)$,通过置换操作使其变为$v_1^N=(s_1,s_3,\cdots,s_{N-1},s_2,s_4,\cdots,s_N)$。

图解如下：

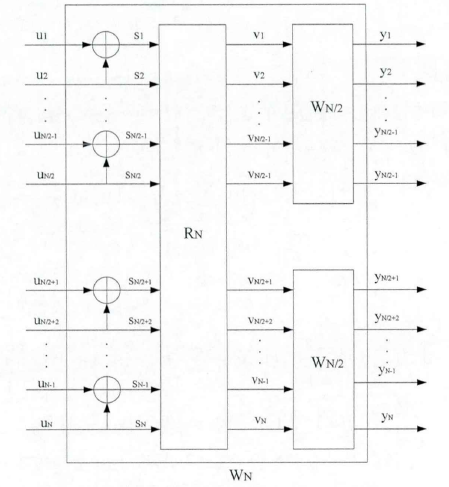
对于一个单独的信道$W:X->Y$来说，它的信道转移概率为$W(Y|X)$。对于具有“集合意义”的$W_N$来说，它的转移概率为$W_N(Y_1^N|u_1^N)$。上述两步变换可以用生成矩阵$G_N$来代替，运算关系为$x_1^N=u_1^NG_N$。于是转移概率变为$W_N(y_1^N|u_1^N)$。这里的向量$x$跟上面说的$v$是一个道理。
这里我们关注转移概率公式的一个细节。公式左边是$W_N$，指代一个由$N$个独立信道合并得到的“信道集合体”。右边是$W^N$，指代$N$个排列在一起但是相互独立的信道。公式的左边很好理解，课将其看做一个单独的信道，$(y_1,\cdots,y_N)$为它的输出，$(u_1,\cdots,u_N)$为它的输入。但是如何理解公式的右边内容？$W^N$表述的是一种怎样的运算？是$W$的$N$次方吗？
答案是，$W^N$代表的是乘积运算，表示$N$个信道的转移概率$W$相乘，但它又不仅仅是相乘。当我们把$W^N$拆成$N$个因子相乘的形式来写的时候，我们必须考虑到生成矩阵在其中所起到的线性变换作用。以$W^2$和$W^4$为例：$W^2(y_1^2|u_1^2)=W(y_1^N|u_1\oplus u_2)W(y_1|u_2)$，这是$W^2$的展开式，我们看到，展开时$u_1$和$u_2$先是根据生成矩阵进行了线性变换，然后才相乘。$W^4$同理：
$W^4(y_1^4|u_1^4)$
$=W_2(y_1^2|u_1\oplus u_2,u_3\oplus u_4)W_2(y_3^4|u_2,u_4)$
$=W(y_1|u_1\oplus u_2\oplus u_3\oplus u_4)W(y_2|u_3\oplus u_4)W(y_3|u_2\oplus u_4)W(y_4|u_4)$
可见，信道合并并未在物理层面上真正的将互不干涉的信道进行了合并，而是通过数学的方法使这些信道产生千丝万缕的联系，形成了一个具有某种“集合意义”的信道集合体。因此下面我们再进行信道分裂的时候也并不是简单地将两个信道分离出来。实际上，因为这些信道一直都是有机的结合在一起，所以信道分裂只是提取出信道在集体中保持的完整的个体属性。正如我们将发现的那样，在集体中的这一特性与原来单独的个体特性已经大不相同，在宏观上这种现象的表现就是信道极化。

信道分裂

所谓信道分裂，其实就是在上述形成的集合体中观察单个信道的属性（主要观察转移概率）。
对于信道集合体中的单个信道来说，它的转移概率通过以下定义来求得：

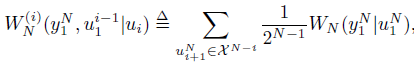
这是一个定义式。从这个式子我们看到，由于原本独立的信道与其他信道有机的结合在了一起，当我们再次观察每个信道时，它们的转移概率将受到其他信道的影响。由于信道合并是一个递归过程，信道分裂作为信道合并的“逆过程”，不可避免的也是一个递归过程。
文献《极化码编码与译码算法研究》（作者：王继伟）中指出，对于上式计算分裂信道的转移概率，其算法复杂度随码长增加呈指数型增加。而将定义式写成如下的迭代式能够使算法具有线性复杂度：

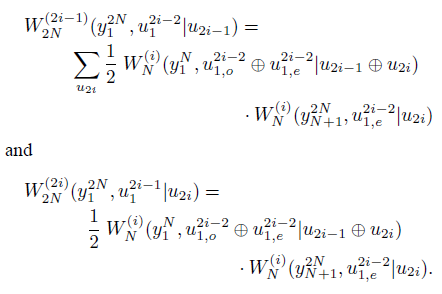
这个公式是通过归纳法得到的。
从信道的合并与分裂的描述中我们可以隐约发现，信道合并与极化码的编码在形式上非常相似，而信道分裂与极化码的解码在形式上非常相似。根据我们对信道合并与分裂的观察，在极化码的仿真体系中：为了完成极化码编码，工作的重点放在生成矩阵的构造；而信道分裂的特殊定义又指明了极化码的译码应该采用串行译码的方式。此外，信道极化现象展示了极化码的宏观特性，通过分析极化现象中的特定参数，我们可以确定极化码编码过程中的信息位选取方案。

信道极化

信道极化是信道合并与信道分裂两种信道操作的结果。在上述两种操作下，原本相同的N个W信道产生了极化现象，其中一部分信道的信道容量趋近于1，另一部分信道的信道容量趋近于0。
这是一个非常特别的现象，因为我们可以利用这种极端的情况，通过在信道容量趋近于1的一部分信道传输有用信息，而在另一部分信道上传递无用信息（即信息量为0的信息），实现对香农限的逼近。
这里是我曾经编写的对信道极化现象进行仿真的matlab代码和结果图：

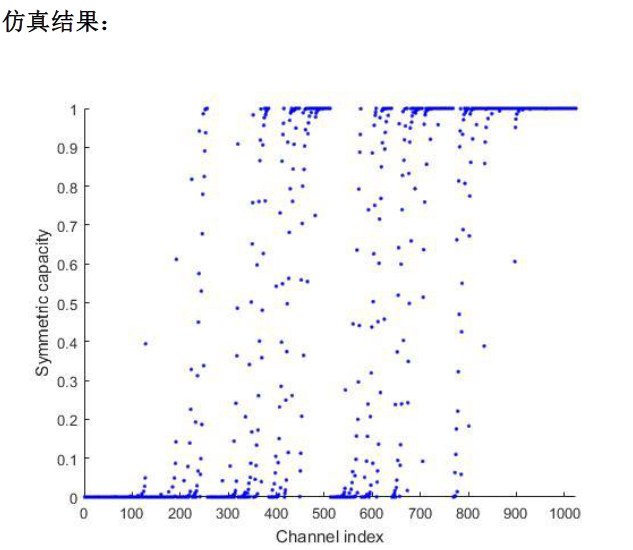
理论依据主要是这个公式：

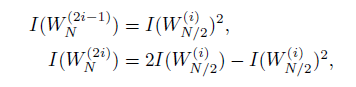
当然不仅仅是这个公式，具体内容请移步论文《channel polarization……》的第【I-B-3) 】节。

极化码的特点

极化码的特点大家应该都已经有所了解，归纳起来主要有两点：

可以到达香农限
什么是香农限？如何到达香农限？到达香农限有什么意义？
香农第二定理（有噪信道编码定理）指出：当信道的信息传输率不超过信道容量时（R≤C），采用合适的信道编码方法可以实现任意低的传输差错。香农第二定理通俗来说就是，在R不大于C的情况下，存在一种能够实现信息的绝对可靠传输的编码方案。而所谓香农限就是同时满足绝对可靠、R逼近C的理想情况。香农第二定理并没有告诉我们如何进行信道编码，但是它指导着我们去寻找更加符合这种理想状态的编码方案，从turbo码到LDPC码，越来越逼近这一理想，而极化码的出现，在理论上实现了这一理想。这种理想的编码方案使我们能够在一个噪声信道中以理论上最小的差错率和最快的速度进行信息传输。
复杂度低
根据Arikan的论文《channel polarization……》中的计算和描述，使用递推方法进行编码和译码的极化码的编码、译码复杂度均为O(NlogN)。这是一个线性复杂度，相对来说其复杂度比较低。复杂度的计算具体位置在论文的VII-C，VIII-A两节，感兴趣者请移步论文。

以上就是对极化码的简单介绍。