希望在旧版博客访问该文章?请戳:极化码小结(2)
极化码的编码问题主要包括两个方面。
生成矩阵的构造
先来看信道合并示意图,下图截自Arikan论文(以后不再解释,Arikan论文 特指论文《Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels》):
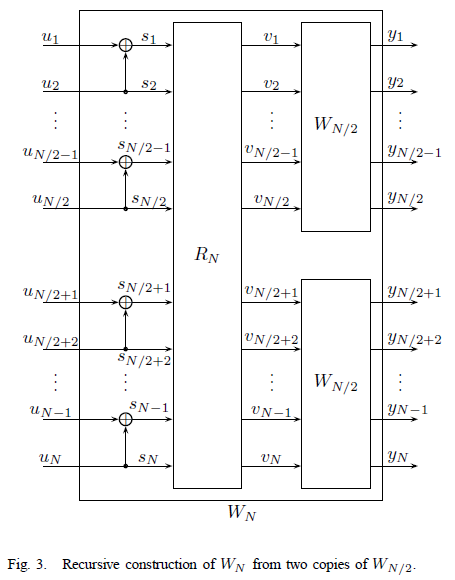
请读者留意这是fig.3,也即图三。根据这张图所表现的形式,我们可以归纳出$G_N$的表达式:
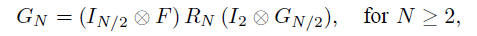
疑问:这个表达式如何得到?它与上图有什么对应关系?
我们来看等式右端第一部分:
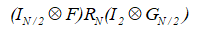
观察$R_N$前面的表达式,符号“$\otimes$”是一种矩阵运算,称为“克罗内克积”,详细内容读者可自行查阅百科词条:克罗内克积-维基百科;“$F$”定义为矩阵$\left[\begin{smallmatrix} 1&0 \\ 1&1 \end{smallmatrix}\right]$。F的定义又有何意义呢?我们用一个二维向量来测试一下:
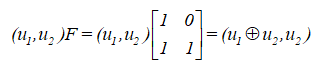
可见用输入向量左乘$F$矩阵,就能够实现图中第一步线性变换。当N>2时,由于F只有二维,为了完成运算,我们通过克罗内克积的办法在保持F矩阵属性的同时扩展它的维度,使得它满足我们的运算要求。所以RN前面的运算可以与上图中的线性变换对应起来。
$R_N$对应图中的自身,这个不需要再说。
观察$R_N$的右端,$I_2$为二维的单位矩阵,$G_{N/2}$则体现了递推、迭代的思想。用$I_2$与$G_N$进行克罗内克积,就是为了实现生成矩阵的递推和迭代。这部分对应了图中最右端的操作。因此我们可以看到,Arikan给出的生成矩阵的定义式确实与上图是完全对应的。
接下来,Arikan又给出了另一张图:
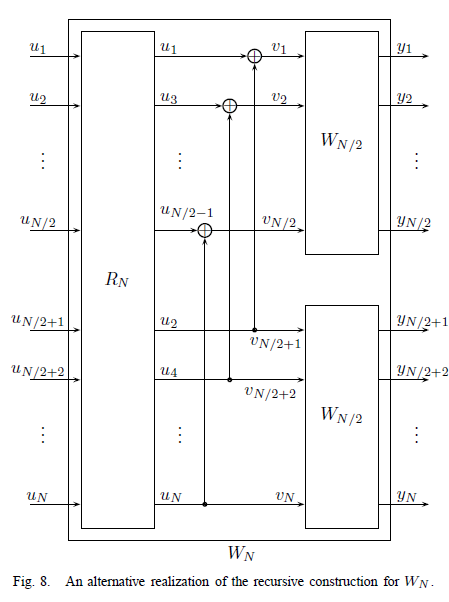
这是fig.8,它与fig.3的不同之处在于,fig.3中先进行线性变换再进行置换操作,而fig.8中先进行置换操作再进行线性变换。根绝Arikan的说法,这两个图是全等的。fig.8对应的公式为:
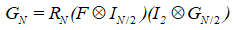
也就是说这两个公式是等价的:
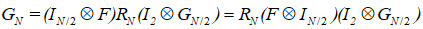
以下为简单的证明过程:

让我们回到Arikan的论文中,继续看他是如何一步一步得到GN的构造方法的。
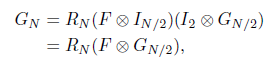
上面这个公式第一行我们已经证明过了,从第一行到第二行的理论支持来自于克罗内克积的混合乘积性质:

继续往下看:
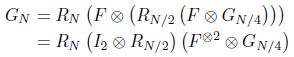
这个就很好理解了,直接迭代代入GN/2然后利用混合乘积性质的逆定理就可以得到了。重复上述操作,不断进行迭代,最后我们可以得到这样一个式子:
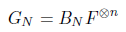
其中$B_N$用来代替迭代所产生的式子为:
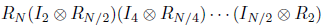
写成递推公式就是:
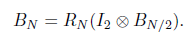
得到上面的公式之后,我们很容易就可以计算出$B_N$并求出$G_N$。
信息位选取
通过上一节的介绍,我们了解到了信道的极化现象,并且认识到正是信道极化现象催生了极化码。现在,我们就要利用这个现象来构造极化码。根据我们所设想的,通过在误差率较低的信道(无噪信道)上传输有用信息,在误差较高的信道(纯噪信道)上传输信息量为0的信息,我们可以实现在有噪信道下进行无噪传输。
因此,如何挑选要传输信息的信道成为了至关重要的事情。在表征信道质量的参数向量P中,我们称传输有用信息的位为信息位,传输无用信息的位为冻结位。问题变成了如何求出这个参数向量$P$。只要我们求得这个$P$,然后对它进行从小到大的排序,再根据码率确定要用到多少信息位,然后从排好序的P中挑选出性能最好的那部分,就可以实现我们的需求。
Arikan的论文中这样说道:“对于一个给定的B-DMC信道$W$,本论文对信道的两个参数感兴趣:一个是信道的对称容量$I(W)$
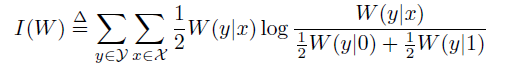
$I(W)$代表了等概率输入下,通过信道$W$进行可靠信息传输的最大速率。第二个称为巴氏参数$Z(W)$
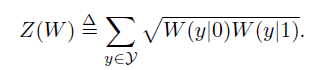
巴氏参数代表了在一次通过$W$传输0或1时,最大似然判决错误概率的上限。显然,$Z(W)$反映了信道的可靠度 。
显然,我们可以分别将这两个参数作为参数向量$P$,对于$I(W)$,我们选择较大的$I(W)$作为信息位;对于$Z(W)$,我们选择较小的$Z(W)$作为信息位。
早期Arikan提出,当$W$为BEC(二进制删除信道)时,有:
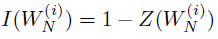
计算二者中的任何一个都可以。Arikan论文中也给出了$Z(W)$的递推计算公式:
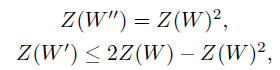
其中第二个式子的不等号在W为BEC取等,因此我们可以精确的计算巴氏参数,而且计算复杂度也较低,为$O(NlogN)$。
后来,Arikan给出了当W不为BEC信道时的计算方法,他提出使用“Monte-Carlo算法”(蒙特卡罗法)来近似计算巴氏参数,然而,这个计算的复杂度因输出符号集的指数型爆炸增长而变得不可能。
还有一种方法也用来进行巴氏参数的估计——Density Evolution(密度进化),但是这个方法缺点在于计算复杂度还是较高(为$O(n)$),同时精确度也不好。
目前我们项目组所使用的信息位选择采用的是tal-vardy所提出的算法。这种算法是Tal和Vardy于2013年发表在IEEE上的一篇21页的论文中提出的,论文名为《how to construct polar code》,感兴趣的读者可以去了解一下。如果对英文阅读感觉到不舒服,读者也可以参考《极化码编码与译码算法研究》[王继伟]在2.2.3节中对这种算法的较为详细的中文介绍。
这种算法主要通过信道弱化和信道强化操作,将输出符号集进行合并,使其能够具有符合我们需要长度的输出符号集大小。另外,对于我们经常用到的AWGN信道,通过高斯近似(GA)方法可以在非常低的复杂度下在较高的精确度上选择信息位。这里列出两篇发表在IEEE上的参考论文,有兴趣的读者可以自行去了解,这里不再展开说了。
【1】《Evaluation and Optimization of Gaussian Approximation for Polar Codes》.Jincheng Dai等.(2016.5)
【2】《Construction and Block Error Rate Analysis of Polar Codes Over AWGN Channel Based on Gaussian Approximation》.Daolong Wu等.(2014.7)
除此之外,还有一种办法可以提高极化码的构造效率。那就是使用“design-SNR”。
不管我们采用什么构造办法,信息位的选取总是与SNR的取值密切相关。我们在仿真极化码性能的时候,往往会以SNR为仿真图的横坐标,以BER、FER为纵坐标,观察曲线走向,通过对比曲线判断优劣。但是每一次带入新的SNR值,都要重新构造一个新的参数向量P,然后重新挑选信息位,这种传统的构造方法我们称为“point-by-point(逐点SNR)”。这种重复性的工作无疑增加了极化码构造的时间复杂度。
通过研究,我们发现,对于一个特定的码率,总存在一个完美的SNR,我们称之为“design-SNR(设计SNR)”,我们只需要代入这个SNR进行一次参数向量P的构造,然后将挑选好的信息位储存起来。以后在这个码率下,不论在哪个SNR值下进行仿真,我们只代入预存的这个信息位进行极化码的构造。由于信息位只构造了一次,时间复杂度得到了显著降低。
根据仿真结果显示,在码长和码块较大的情况下,design-SNR与point-by-point法契合的非常好,如下图:
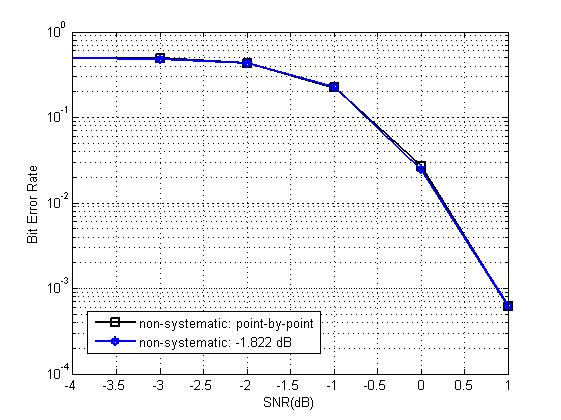
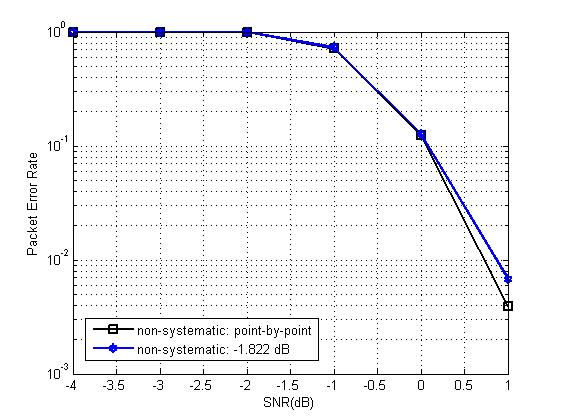
得到了生成矩阵,又构造了信息位。接下来只需要进行简单的矩阵操作,再叠加上噪声,就可以实现极化码的编码。
转载请注明来源:©Tinshine